비용 함수 E(w) 최소화하는 w를 구하는 문제에 대해 학습률을 크게 설정하여 경사 강하법 알고리즘을 작성하다
학습률이 큰 경우 (eta=0.4)
E(w) = 3(w-2)^2 +5eta = 0.4, w1=5
초기비용함수 E(w1) = 3(5-2) ^2 +5 =32
dE/dw = 6(w-2)
10회 반복 w2=w1-eta*(dE/dw)*w1=5-0.4*6*(5-2)=-2.2 비용 함수 E(w2)=57.92w3=w2-eta*(dE/dw)*w1=-2.2-0.4*6*(-2.2-2)=7.88 비용 함수 E(w3)=108.7232
…
w11 = w10-eta*(dE/dw)*w10 =-59.9831-0.4*6*(-59.9831-2) =88.7764 비용함수E(w11)=22595.428965
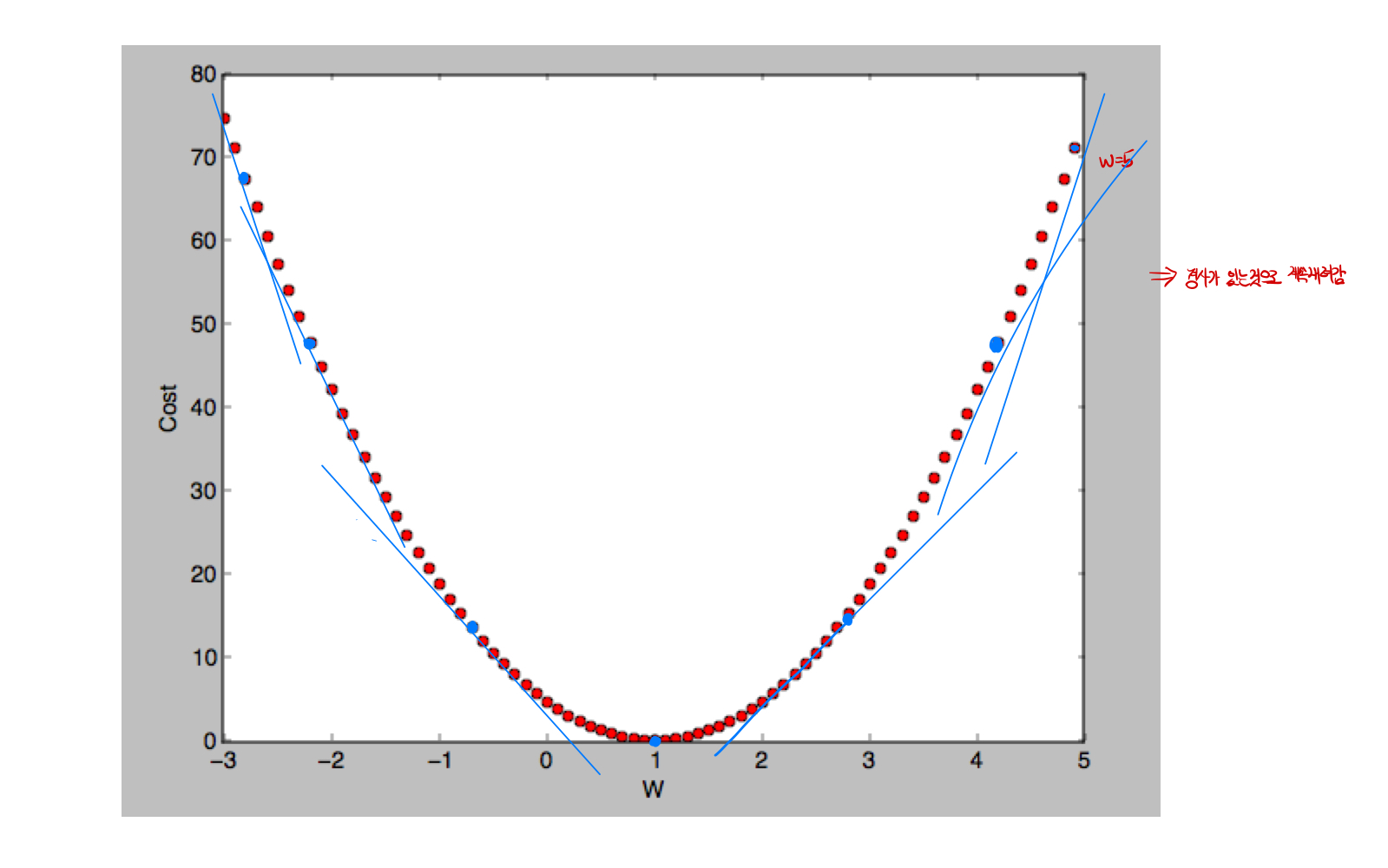
함수값 E(w(n))가 점점 커진다 => 비용함수를 최소화하는 값에서 더 멀어짐을 반복 => w(n) 발산하다
비용함수 E(w) 최소화하는 w를 구하는 문제에 대해 학습률을 작게 설정하여 경사강하법 알고리즘을 작성하는 학습률이 작은 경우 (eta=0.01)
E(w) = 3(w-2)^2 +5eta = 0.01, w1=5
초기비용함수 E(w1) = 3(5-2) ^2 +5 =32
dE/dw = 6(w-2) 10회 반복 w2 = w1-eta*(dE/dw)*w1 = 5-0.01*6*(5-2) = 4.82 비용 함수 E(w2)= 28.8572w3 = w2-eta*(dE/dw)*w1 = 4.82-0.01*6*(4.82-2) = 4.6508 비용 함수 E(w3) = 26.080222
…
w11 = w10-eta*(dE/dw)*w10 = 3.718984-0.01*6*(3.718984-2) = 3.615845 비용함수 E(w11)= 12.832869
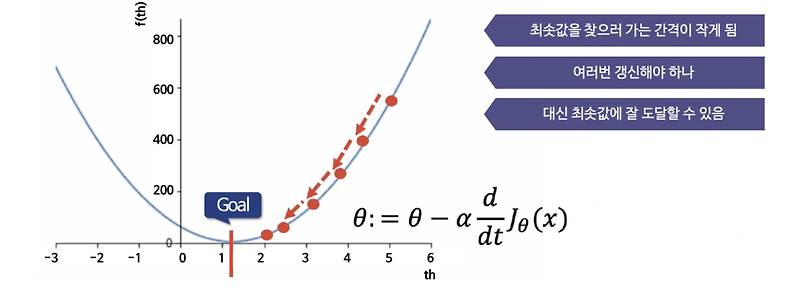
학습률이 너무 작으면 수렴 속도가 느려지고 계산량이 많아 학습 속도가 느려진다.
비용함수 E(w) 최소화하는 w를 구하는 문제에 대해 학습률을 적절히 설정하고 경사강하법 알고리즘을 작성하는 학습률이 적절한 경우 (eta=0.1)
E(w) = 3(w-2)^2 +5eta = 0.1, w1=5
초기비용함수 E(w1) = 3(5-2) ^2 +5 =32
dE/dw = 6(w-2) 10회 반복 w2 = w1-eta*(dE/dw)*w1 = 5-0.1*6*(5-2) = 3.2 비용 함수 E(w2)= 9.32w3 = w2-eta*(dE/dw)*w1 = 3.2-0.1*6*(3.2-2) = 2.48 비용 함수 E(w3) = 5.6912
…
w11 = w10-eta*(dE/dw)*w10 =2.000786 -0.1*6*(2.000786-2) =2.000315
비용함수 E(w11)=5.0
신속하고 정확하게 수렴