최근 회사 업무에서 부품 샘플의 전압 편차가 파워 편차로 어떻게 나타나는지 계산해야 할 일이 있었습니다. 제가 통계에 대해 무지하지만 다행히 통계학과 출신 아내가 있어서 잘 해결됐습니다 이것을 계기로 저도 통계학을 알아야겠다고 생각했습니다 생각보다 너무 쉽고 재미있게 책이 쓰여 있어서 앉은 자리에서 다 읽었어요.
이 책에서 가장 재미있게 읽었던 부분은 ‘몬티홀 문제’였어요 제가 간단하게 옮겨봤어요.
몬티홀은 ‘미국 인기 게임쇼 Let’s make adeal’ 진행자 이름입니다. 이 프로그램에서는 시청자 앞에 놓인 3개의 문 중에서 자동차 상품이 놓인 문을 선택하면 상품을 획득할 수 있는 프로그램이었다고 해요. 여기서 프로그램의 재미를 높이기 위해 시청자가 하나를 선택하면 사회자는 나머지 두 문 중 꽝에 해당하는 문을 열어 보이면서 나머지 문으로 바꿀 것인지, 아니면 처음에 자신이 선택한 문을 고수할 것인지 묻습니다. 언뜻 보면 무엇을 선택하든 확률은 1/2처럼 보입니다. 하지만 당시 IQ 228로 알려져 있는 마릴린의 생각은 달랐다고 합니다. 그녀는 “몬티홀 문제로 문을 바꾸면 당첨될 확률이 두 배가 됩니다”라고 말한 겁니다. 그녀는 당시 수학자를 포함한 많은 사람들로부터 비난을 받았다고 합니다. 한 수학자가 컴퓨터 시뮬레이션을 이용해서 그녀의 주장이 맞았음을 증명했어요.
어떻게 된 일일까요? 극단적인 사례를 들어본다면 이해할 수 있을 거예요. 문이 100개라고 생각해봅시다. 첫 번째 시청자가 문을 하나 선택하면 그 문이 정답일 확률은 1/100, 99개의 문 중 하나가 정답일 확률은 99/100입니다. 이때 남은 문 98개를 삭제하면 사회자가 남긴 1개의 문이 가질 확률은 99/100이 됩니다.
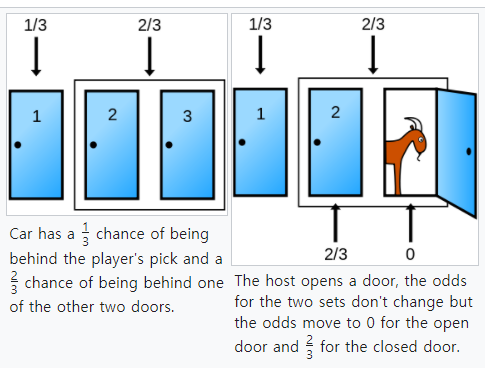
https://en.wikipedia.org/wi ki/Monty_Hall_problemMonty Hall problem From Wikipedia, the free encyclopedia The Monty Hall problem is a brain teaser, in the form of a probability puzzle, loosely based on the American television game show Let’s Make a Deal and named after its original host, Monty Hall . The problem was originally posed (and solved) i…en.wikipedia.org
또 하나 재미있는 내용은 홍차부인의 에피소드입니다. 어떤 부인이 홍차를 맛보면 우유와 홍차 중 어느 것을 먼저 컵에 넣었는지를 구별할 수 있다고 주장한다면 어떻게 진위를 가릴 것인가 하는 문제입니다. 다시말해서맞힐확률이1/2이기때문에몇번연속해서,혹은몇번중에몇번맞히면우연이아니라실력으로인정받을수있는가라는문제입니다. 여기서 중요한 것은 우연과 실력을 가르는 기준인데요. 귀무 가설에 근거해 쉽게 일어나지 않는 우연이라면 실력으로 규정하는 겁니다. 통계적 유의성을 나타낼 때 보통 5%의 확률을 그 기준으로 삼는데 일어날 확률이 5% 미만이면 실력으로 봐도 된다는 것입니다 아래 표는 1/2의 확률의 이항 분포를 나타내고 있습니다. 8~10까지 더하면 약 5.5%입니다. 홍차 부인이 홍차를 약 10회 끓였을 때 8회 이상 끓일 확률이 5.5% 이내라고 합니다. 즉 홍차 부인이 10번 중 8번 이상 맞추었다면 실력을 인정해도 좋지 않을까 하는 것이군요.
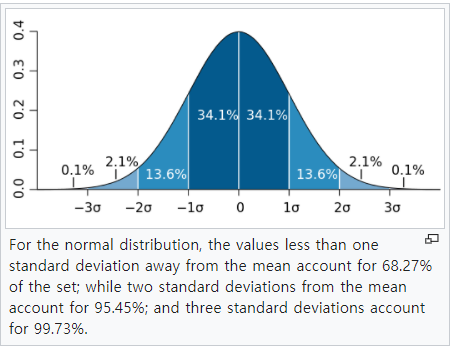
https://www.thoughtco.co m / binomial – table – n-10 – n-11 – 3126257 See a binomial distribution table for n = 10 and 11 and a variety of probabilities.www.thoughtco.com
다음은 제가 이해한 내용을 정리해 보았습니다.
- 정규 분포
- 정규 분포곡선에서 ‘평균 +/-표준편차’까지의 범위는 특정 데이터가 해당 범위에 포함될 확률을 나타냅니다.
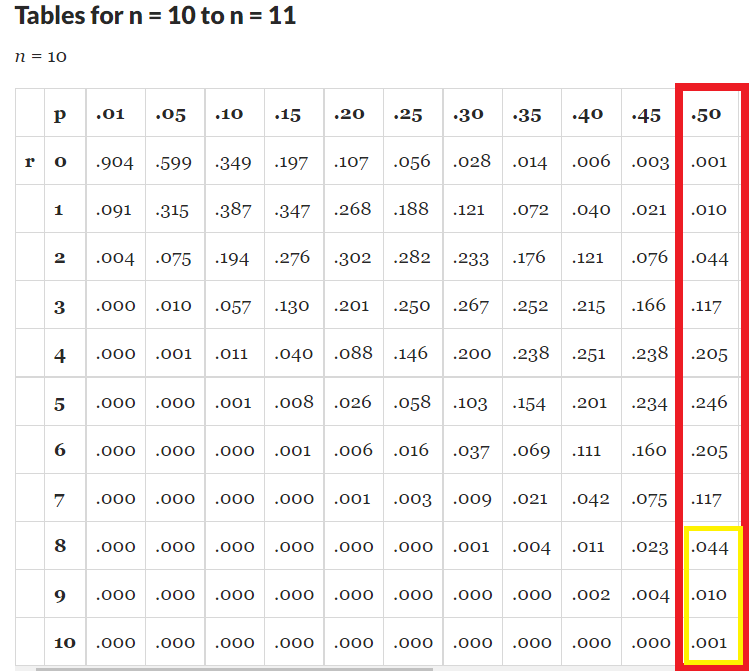
평균에서 +/-1시그마(표준편차) 안에 들어갈 확률은 68.27% 평균에서 +/-2시그마(표준편차) 안에 들어갈 확률은 95.73% 평균에서 +/-3시그마(표준편차) 안에 들어갈 확률은 99.73%
그러나, 보통 95%와 99%의 확률과 같이 딱 맞는 숫자를 사용하기 때문에, 95%의 표준 편차는 1.96 시그마, 99%의 2.58 시그마를 잘 사용합니다.
2. 표본을 이용하여 모집단이 특징 추정하는 말 그대로 여러 표본의 평균을 이용하여 모집단의 성격을 파악하는 방법입니다. 책에서는 과수원의 사과를 예로 들고 있습니다. 과수원의 사과를 여러 사람에게 똑같이 10개씩 나누었다면 각 개인이 받은 사과의 평균 중량으로 히스토그램을 그리면 정규 분포를 그리게 됩니다. 이렇게표본평균의분포를이용하는것을중심극한정리라고합니다.
<중심 극한 정리 – Central Limit Theorem>3, 시청률 추정 시청률은 95% 구간 추정 시 다음과 같은 방법으로 구할 수 있습니다.p는 조사에 의한 시청률, n은 추출 세대수로 하면…
이때 시청률은 정규분포가 아닌 이항분포이므로 표준편차가 sqrt(p*(1-p))로 계산됩니다.여기서 p를 당기면 표본오차가 있어요.
선거를 치르고 출구조사를 하면 95% 신뢰수준, 오차범위는 어떻게 된다는 게 이런 뜻입니다.
#이렇게쉬운통계학 #서평 #알기쉬운 #통계학 #몬티홀문제 #MontyHallProblem #홍차부인 #시청률